この記事でやりたいこと
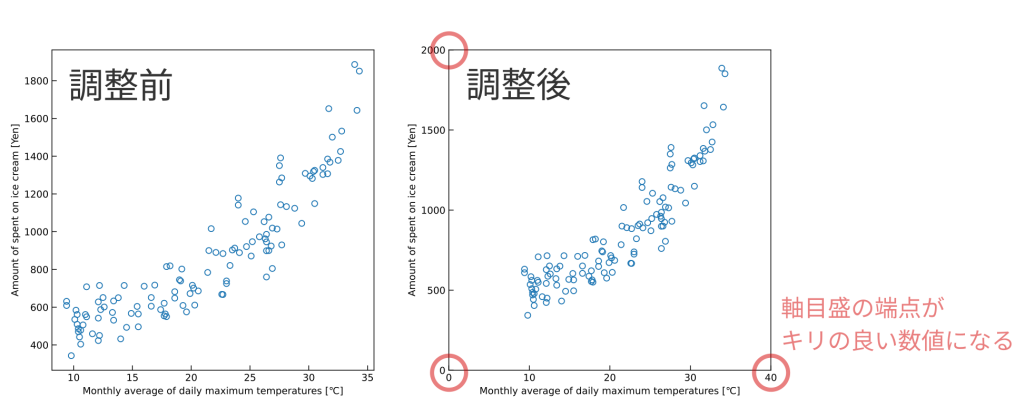
データ範囲から軸目盛の範囲と間隔を自動調整し、
端点がキリの良い数値になる美しいグラフを描画します。
コードは Python ですが、他の言語でも同様にして実装可能です。
背景
軸目盛の両端がキッチリした数値になるグラフが美しいですよね。
少数のグラフであれば手作業で調整しても良いですが、まとまった量のグラフを描く場合には軸目盛の範囲と分割数を自動で決められたら便利だと思ったのがきっかけです。
軸目盛の自動調整アルゴリズムについては、既に考案および実装されている方がいます[1][2][3]。
本記事では、Python での実装と考え方についてまとめます。
軸目盛の自動調整
実行環境
今回の環境は下記の通りです。
よほど古くなければ同じように動くと思います。
| Python | 3.12.2 |
| Matplotlib | 3.8.4 |
コード
データ範囲を入力とし、軸目盛の端点値と分割数を返すメソッドの実装例です。
import math
from typing import Optional, Tuple, Union
def auto_ticks(
vmin: float,
vmax: float,
margin: Optional[Union[float, Tuple[float, float]]] = None,
) -> Tuple[float, float, int]:
"""
データ範囲に応じた軸目盛を自動で決定する。
Parameters
----------
vmin : float
データの最小値
vmax : float
データの最大値
margin : Optional[Union[float, Tuple[float, float]]]
データの最小値や最大値が軸目盛の端点と一致するのを避けるためのパラメータ。
端部で余裕度が欲しい場合、入力データのスケールで指定する。
指定がない場合、マージンは 0 とする。
Returns
-------
tick_params : Tuple[float, float, int]
決定した軸目盛のパラメータ。 (tmin, tmax, tsep) の順番で返す。
Raises
------
TypeError
マージンの指定方法に誤りがある場合。
単一の数値または要素数2の Iterable オブジェクトで指定する必要がある。
Notes
-----
取得したパラメータから np.linspace(tmin, tmax, tsep) を使用すると軸目盛を設定しやすい。
"""
# スケール変換
vmin, vmax = sorted([vmin, vmax]) # 大小関係が逆の場合は修正
width = vmax - vmin # データ範囲
n_digit = math.floor(math.log10(width)) # データ範囲の桁数 - 1
scale = 10 ** n_digit # データ範囲を [1, 10) に変換するための係数
# 最適な目盛間隔の計算
d_ticks = (0.2, 0.5, 1, 2) # 目盛間隔の候補リスト
d_candidates = [d for d in d_ticks if d <= (width / scale / 2)] # 条件 2d <= w を満たす目盛間隔を抽出
d_tick = scale * d_candidates[-1] # その中で最大の間隔を取得, スケールを復元
# 引数 margin の処理
if margin is None:
mmin, mmax = (0, 0)
elif isinstance(margin, float):
mmin, mmax = (margin, margin)
elif len(margin) == 2:
mmin, mmax = margin
else:
raise TypeError('margin must be a numerical type or an iterable object with two numerical elements')
# 軸目盛の範囲と分割数の計算
tmin = d_tick * math.floor((vmin - mmin) / d_tick) # 目盛の最小値
tmax = d_tick * math.ceil((vmax + mmax) / d_tick) # 目盛の最大値
tsep = int(tmax / d_tick - tmin / d_tick) + 1 # 目盛の分割数
tick_params = (tmin, tmax, tsep) # 結果をまとめてタプル化
return tick_params解説
スケール変換
width = vmax - vmin # データ範囲
n_digit = math.floor(np.log10(width)) # データ範囲の桁数 - 1
scale = 10 ** n_digit # データ範囲を [1, 10) に変換するための係数与えられるデータによってスケールが異なるので、まずはデータ範囲の桁数を調べます。
桁数をもとに、データ範囲を1以上 10 未満の範囲にスケール変換します。
データ範囲 \( {\rm width} \) の桁数 \(n\) について、次の関係が成り立ちます。
データ範囲が小数の場合も同様に処理できます。
\( {n – 1} \leq \log_{10}{\rm width} < n \) …①
\( 10^{n – 1} \leq {\rm width} < 10^{n} \) …②
①式から、変数 \(n_{\rm digit} = \lfloor \log_{10}{\rm width} \rfloor = n – 1 \) になります。
②式の辺々を変数 \( {\rm scale} = 10^{n_{\rm digit}} = 10^{n-1} \) で除算すると、次のようになります。
\( 1 \leq \frac{\rm width}{\rm scale} < 10 \) …③
したがって、データ範囲 \( {\rm width} \) を \( {\rm scale} \) で割ることで、1 以上 10 未満の範囲にスケール変換することができます。
最適な目盛間隔の計算
d_ticks = (0.2, 0.5, 1, 2) # 目盛間隔の候補リスト
d_candidates = [d for d in d_ticks if d < (width / scale / 2)] # 条件 2d < w を満たす目盛間隔を抽出
d_tick = scale * d_candidates[-1] # 候補のうち最大の目盛間隔を取得かつスケール復元グラフに少なくとも2つの目盛がないと、値を読み取ることができません。
また、7刻みなどキリの悪い刻み方はすべきではありません。
今回は、下記の条件を同時に満たす最大の値を目盛間隔 \( d’_{\rm tick} \) とします。
\( d’_{\rm tick} < \frac{w’}{2} \) を満たす値 …Ⓐ
\(1, 2, 5\) に \( 10^k (k \in \mathbb{Z}) \) を掛けた値 …Ⓑ
条件Ⓐは、目盛が2つ以上存在するための条件です。ここで、\( w’ = \frac{\rm width}{\rm scale} \) はスケール変換後のデータ範囲、\(d’_{\rm tick}\) はスケール変換後の目盛間隔です。
条件Ⓑは、目盛の刻み幅がキリの良い数字であるための条件です。通常の線形軸であれば、このように設定すれば問題ないと思います。
条件Ⓑに対して、コード上の候補リストは 0.2 始まりで少し違った形をしています。これは、式③から \( 0.5 \leq \frac{w’}{2} < 5 \) であり、\(d’_{\rm tick}\) がとりうる値は \( (0.2, 0.5, 1, 2) \) のいずれかとなるためです。
\( 1 \leq w’ < 10 \) …③(再掲)
条件を満たす目盛間隔の候補が複数存在する場合、最大のものを選択することにします。
決定した \(d’_{\rm tick}\) はスケール変換後の目盛間隔なので、元に戻した \(d_{\rm tick} = {\rm scale} \times d’_{\rm tick}\) を最終的な目盛間隔とします。
軸目盛の範囲と分割数の計算
tmin = d_tick * math.floor((vmin - mmin) / d_tick) # 目盛の最小値
tmax = d_tick * math.ceil((vmax + mmax) / d_tick) # 目盛の最大値
tsep = int(tmax / d_tick - tmin / d_tick) + 1 # 目盛の分割数目盛間隔が決まったので、グラフ枠の端点に目盛が重なるように軸の最小値と最大値を求めます。
軸目盛の端点をキリの良い数値にしたいので、軸目盛間隔の整数倍となる近隣の点を求めます。
ここでは軸の最小値を用いて説明します。
軸目盛の最小値 \( t_{\rm min} \) は、データの最小値より小さい側の最寄りの整数点とします。これは床関数を使用して求めることができます。
調整パラメータ \(m_{\rm min} \) は、\( \frac{v_{\rm min}}{d_{\rm tick}} \) が整数の場合に端点とデータ点が一致してしまうのを防ぐためのパラメータです。その他の場合にも、描画範囲を微調整したい場合に使用できます。
イメージは下図の通りです。

プログラムの実行
サンプルデータ
総務省統計局のWebサイト[4] からデータをお借りしました。
東京都の最高気温の月平均とアイスクリームの支出金額の散布図用データ(e13.xlsx)です。
感覚的には、気温とアイスクリームの購入量は正の相関がありそうですね。
import pandas as pd
path = 'e13.xlsx'
df = pd.read_excel(path, skiprows=2)データの中身はこんな感じです。
日付列がシリアル値になっていますが、今回は使わないので無視します。
| 時間軸\n(月次) | 日最高気温の月平均(℃) | アイスクリームの支出額(円) | |
| 0 | 41640 | 10.6 | 404 |
| 1 | 41671 | 9.8 | 343 |
| 2 | 41699 | 14.5 | 493 |
| … | … | … | … |
| 119 | 45261 | 14.3 | 715 |
x 軸と y 軸に使うデータをそれぞれ取り出しておきます。
x = df['日最高気温の月平均(℃)']
y = df['アイスクリームの支出額(円)']動作確認
まずは、軸目盛の範囲を指定せずにプロットしてみます。
fig, ax = plt.subplots(figsize=(6, 6))
ax.scatter(x, y, fc='None', ec='tab:blue') # 塗りつぶしなしで青枠のマーカー
ax.set_xlabel('Monthly average of daily maximum temperatures [℃]') # xラベルは気温
ax.set_ylabel('Amount of spent on ice cream [Yen]') # yラベルは支出金額
ax.tick_params('both', direction='in', length=5) # 両軸とも内向き目盛
plt.show()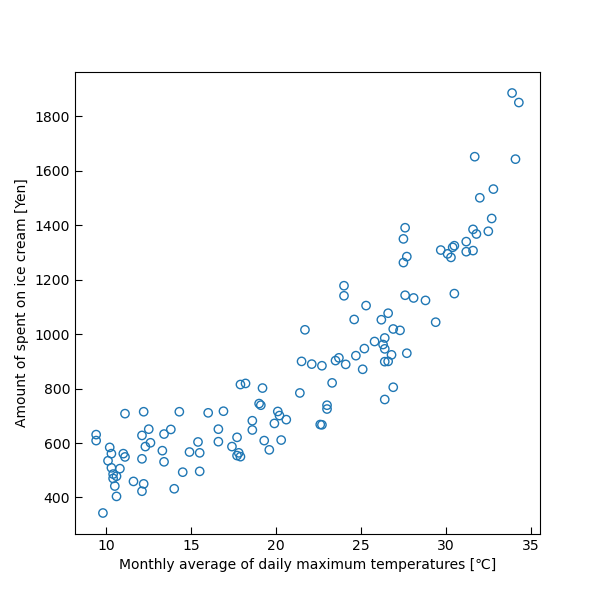
軸目盛の位置はあまり綺麗ではありませんが、描画範囲はデータに合わせてくれますね。
次に、軸目盛を自動調整してみます。
fig, ax = plt.subplots(figsize=(6, 6))
ax.scatter(x, y, fc='None', ec='tab:blue') # 塗りつぶしなしで青枠のマーカー
ax.set_xlabel('Monthly average of daily maximum temperatures [℃]') # xラベルは気温
ax.set_ylabel('Amount of spent on ice cream [Yen]') # yラベルは支出金額
ax.tick_params('both', direction='in', length=5) # 両軸とも内向き目盛
# x軸目盛の調整
xmin, xmax, xsep = auto_ticks(x.min(), x.max())
ax.set_xlim(xmin, xmax) # 描画範囲の設定
ax.set_xticks(np.linspace(xmin, xmax, xsep)) # 軸目盛の設定
# y軸目盛の調整
ymin, ymax, ysep = auto_ticks(y.min(), y.max())
ax.set_ylim(ymin, ymax) # 描画範囲の設定
ax.set_yticks(np.linspace(ymin, ymax, ysep)) # 軸目盛の設定
plt.show()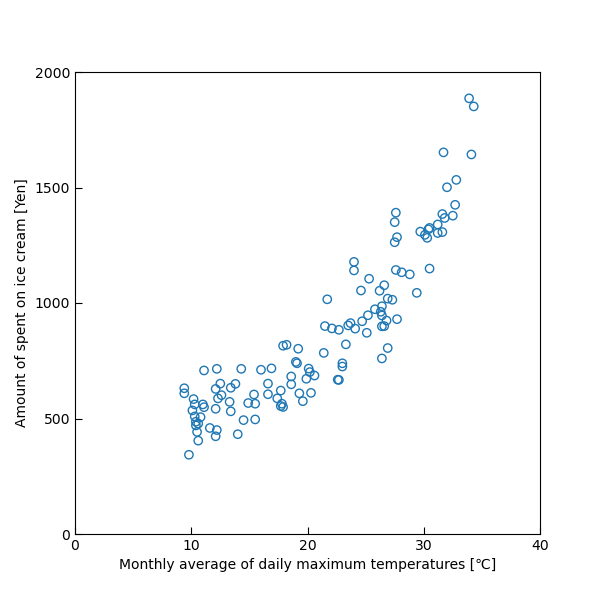
軸の両端が良い感じになりました。
データを眺めるだけならデフォルトの方が良い場合もありそうですが、
資料に載せるような場合はこちらの方が見栄えは良いですね。
参考サイト
[1] 野本隆宏さん | 新潟大学, グラフの目盛り間隔の求め方(2024/8/21 アクセス)
https://www.eng.niigata-u.ac.jp/~nomoto/21.html
[2] しゅんたろうさん | アメブロ, データに合わせてグラフの目盛りを自動で決める(2024/8/21 アクセス)
https://ameblo.jp/hiromi-0505/entry-12580621059.html
[3] yo16さん | Qiita, グラフの軸は意外と難しい(2024/8/21 アクセス)
https://qiita.com/yo16/items/ea620dc234286130e348
[4] 総務省統計局 | 暑い日にアイスクリームは売れる?(2024/8/21 アクセス)
https://www.stat.go.jp/naruhodokids/graph/is-e5-static.html

コメント